점근적 표기법 형태의 함수
ko.khanacademy.org
*이 게시물은 위 링크의 글을 필사하거나 요약한 글입니다.
점근적 표기법을 사용할 경우, 알아야 할 몇 가지
(1)알고리즘이 입력 크기와 상관없이 일정한 시간이 소요된다고 가정합니다. 예를 들어 오름차순으로 정렬된 배열이 있습니다. 여기서 최솟값을 찾아야합니다. 최솟값은 인덱스 0번에 위치함으로 이 알고리즘은 입력 크기에 상관없이 일정한 시간이 소요됩니다.
위 n의 함수를 점근적 표기법으로 표현하면 어떻게 표현할수 있을까요? 세타(n의0제곱)만큼의 시간에 실행된다고 표현할 수 있습니다. n의0제곱은 1이기 때문입니다. 그러므로 알고리즘의 실행 시간은 상수값이 1 이내가 됩니다. 실제로 표현할땐 세타(1)이라고 쓰면됩니다.
(2)알고리즘에 세타(log10n)시간이 소요된다고 가정합니다. 알고리즘이 Θ(log2n)걸린다고 볼 수도 있습니다. 로그의 밑이 상수라면 점근적 표기법에서 어떤 밑 값을 사용하는지는 문제가 되지 않습니다.

위 식은 모든 양수 a,b,n에 대해서 성립합니다. 만일 a와 b가 상수라면 log a n과 log b n은 log b a에 의해서만 달라집니다. 이는 점근적 표기법에서 무시할수있는 상수값입니다(?)
그러므로 이진 검색의 최대 실행 시간은 모든 양수 값인 a에 대하여 세타(log a n)이라고 말할 수 있습니다. 이진검색의 최대 추측횟수는 log2n+1번인데 추측을 하고 테스트하는 과정, 반복문을 설정하고 반환하는 시간은 상수이기 때문입니다.
ps. 보통 이진 검색은 Θ(log2n) 시간이 걸린다고합니다. 이는 대부분의 컴퓨터 공학자들이 2의 제곱으로 수를 세기를 좋아하기 때문입니다.
어떤함수의 실행 시간이 더 클까
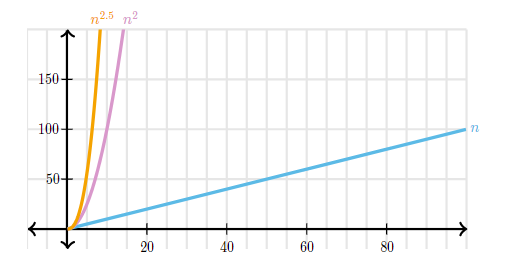
알고리즘을 분석할 떄 종종 사용하는 함수들의 순서가 있습니다. a와 b가 상수이고 a<b라면 세타(n^a)의 실행 시간은 세타(n^b)의 실행시간보다 천천히 커집니다. 아래 그래프에는 n, n^2, n^2.5가 증가하는 정도를 비교합니다.
로그 함수의 경우 다항식보다 더욱 천천히 증가합니다. 즉 Θ(log2n)은 모든 양의 상수 a에 대하여 세타(n^a)보다 천천히 증가합니다. 그렇지만 n이 커지면 log2n의 값도 커지기 때문에 세타(1)보다는 빨리 커집니다. 아래의 그래프는 1, n, log2n이 증가하는 정도를 비교하는 그래프입니다.

자주보게 되는 함수의 실행 시간 성장률의 순위

ps. a>1일 떄 지수 함수 a^n은 b가 상수인 모든 다항식 함수 n^b보다 빨리 커집니다.