개요
병합정렬의 분할 정복 세 단계와 그것의 소요시간을 어떻게 계산해야하는지 살펴봅니다. 전체 배열에서 n 개의 요소를 정렬한다고 가정하겠습니다.
1. 분할 단계는 하위 배열의 크기에 상관없이 일정한 시간이 걸립니다. 결국 분할 단계는 인덱스 p 와 r 의 중심점인 q 를 계산합니다. big-Θ 표기법에서 Θ(1)로 소요시간을 나타냈다는 것을 기억하세요.
2. 각각 n/2개의 요소를 가진 두 개의 하위 배열을 재귀적으로 정렬하는 정복 단계에도 어떤 시간이 걸립니다. 하지만 이는 하위 문제를 계산할 때에 함께 계산하겠습니다
3. 결합 단계에서 Θ(n) 시간 동안 총 n개의 요소를 병합합니다.
분할 단계와 결합 단계 소요 시간
분할과 결합단계를 보면, 분할 단계는 Θ(1) 입니다. 결합 단계는 Θ(n) 입니다. 분할 단계의 소요 시간이 결합 단계보다 낮은 차수의 항이기 때문에 분할 단계와 결합 단계를 합하여 Θ(n) 시간이 걸린다고 생각하겠습니다. 확실하게는 어떤 상수 c*n 만큼 걸리겠지만요.
문제를 간단히
소요시간을 구하기 위해, 문제를 간단히 하겠습니다. n>1보다 항상 크고 항상 짝수라고 가정하겠습니다. 이렇게 해도 빅세타 관점에선 값이 달라지지 않기 때문입니다.
고로 n 요소를 가진 하위 배열에서 mergeSort를 실행하는 시간은 (n/2) 요소를 가진 하위 배열에서 mergeSort 를 실행하는 시간(정복 단계)의 두 배와 c*n(분할 단계와 결합 단계)을 합한 시간이라 생각할 수 있습니다.
그럼 n/2 요소에서 두 번의 재귀적 호출을 실행하는데 드는 시간에 대해 알아봐야겠네요. 이 두 재귀적 호출 각각에는 (n/2를 반으로 나누어야 하기 때문에)(n/4) 개 요소의 하위 배열에 mergeSort를 실행하는 시간의 2배에, 병합하는데 드는 cn/2를 더한 시간이 소요됩니다. n/2 크기의 두 개의 하위 문제가 있고, 각각은 병합하는데 cn/2 시간이 들기 때문에 n/2 크기의 하위 문제를 병합하는데 드는 총 시간은 2*cn/2 = cn 입니다.
트리로 그려본 병합 시간

컴퓨터 공학자들은 트리를 실제 나무가 자라는 것과 반대로 그립니다. 트리는 사이클(같은 장소에서 시작하고 끝나는 경로)이 없는 그래프입니다. 통상 트리에서의 정점을 노드라고 부릅니다. 루트 노드는 가장 위에 놓입니다. 루트에는 n개 요소를 가진 n 크기인 원래 배열의 하위 배열 크기가 표시됩니다 아래 그림에서 루트는 두 자식 노드가 있는데 각각의 크기가 n/2 인 두 하위 문제이므로 n/2 로 표시합니다
크기 n/2의 하위 문제에서는 크기 (n/2)/2 또는 n/4의 두 하위 배열을 재귀적으로 정렬합니다. 크기 n/2의 하위 문제는 2개이므로 n/4크기의 하위 문제는 네 개가 있습니다. 네 가지 하위 문제 각각은 총 n/4개의 항목을 병합하기 때문에 네 개의 하위 문제 모두를 병합하는 시간은 cn/4가 됩니다. 4개 하위 문제의 총 시간을 합하면 n/4 크기의 하위 문제 모두를 벼합하는 시간이 4*cn/4 = cn 라는 것을 알 수 있습니다.

n/8 크기의 하위 문제에서는 어떻게 될까요? 마찬가지 입니다. 8*cn/8 = cn 이 될겁니다.
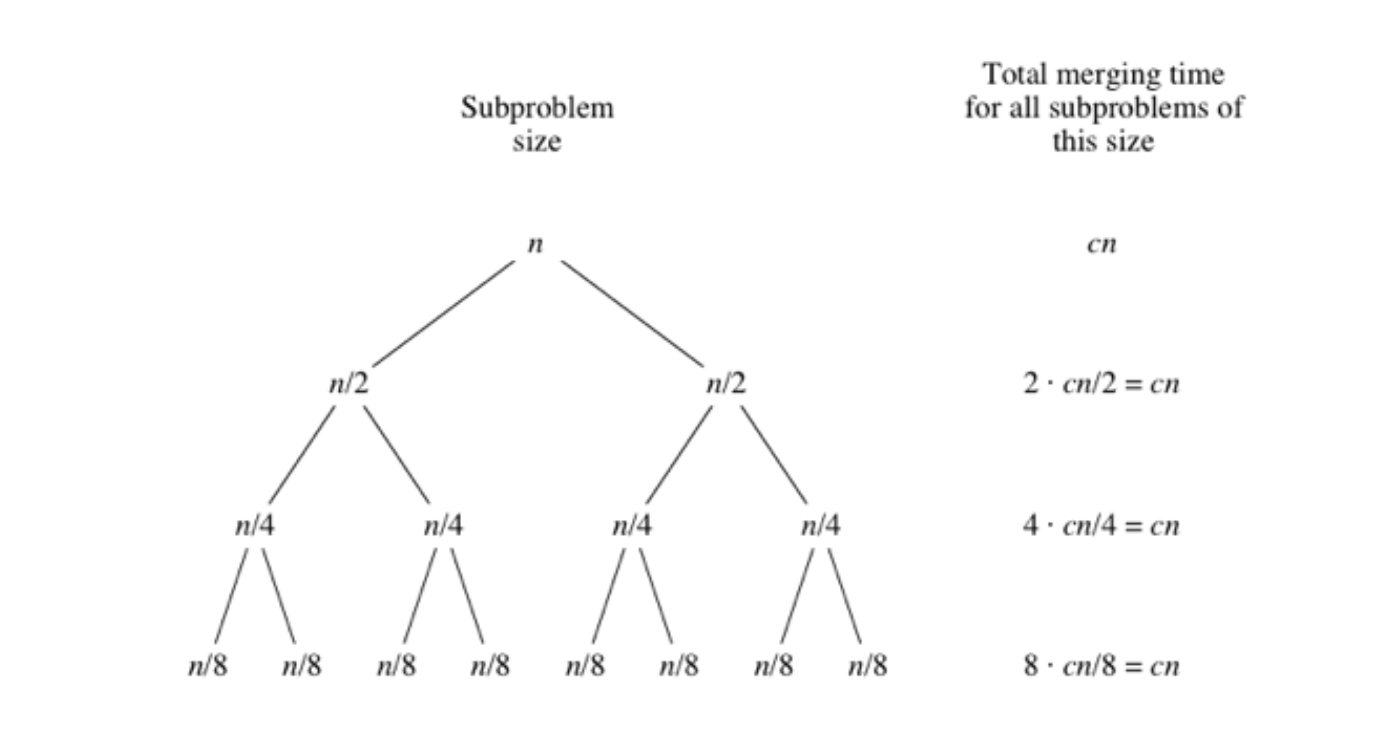
하위 문제가 작아질수록 하위 문제의 수는 재귀과정의 각 단계마다 배가 됩니다. 하지만 병합 시간이 반으로 줄게됩니다. 재귀는 배가 되지만 병합 시간이 절반이 되기 때문에 결국은 재귀 단계에서 총 병합시간은 cn에 그칩니다. 이렇게 계속 재귀가 반복되어 크기 1의 하위 배열이란 탈출 조건에 도달하게 됩니다.
크기 1의 하위 배열을 정렬하려면 p < r 인지 여부를 검사해야 하고, 이 과정에서 세타(1) 시간이 소요됩니다. 크기 1의 하위배열이 몇 개나 있을까요? 처음 시작할 때 n 개 요소로 시작했으므로 하위 배열도 n 개 있을겁니다. 고로 각각의 탈출 조건을 모두 합하면 cn 시간이 걸립니다.

이제 각 하위 문제 크기에서 병합 과정에서 얼마나 걸릴지 알게 됐습니다. mergeSort에 소요되는 총 시간은 모든 단계에서의 벼합 시간을 합한 것입니다. 트리에 i 레벨이 있다면 총 i*cn입니다. 여기서 i 는 무엇을 의미할까요. 지금까지 n 크기 문제의 하위 문제로 시작해서 하위 무넺가 1로 줄어들 때까지 반복적으로 이를 반으로 줄였습니다.
이런 특징은 이진 검색을 분석 할 때 본 적이 있습니다. 이에 답은 i = log2n+1이 됩니다. 예를 들어 n = 8 이면 log2n+1 = 4이고 트리는 n = 8,4,2,1의 4레밸로 이루어지게 됩니다. 그러면 mergeSort에 드는 총 시간은 cn(log2n+1)입니다.
이 시간을 빅세타 표기법으로 나타내면 낮은 차수항 +1 을 제하고, 상수 계수 c 를 제하면 n*log2n 이 소요시간이 됩니다.
병합 정렬의 또 다른 사실
병합 과정 중 정렬된 전체 배열은 두 개의 배열로 나눠지고 복사본을 만들게 됩니다. 상수 개수보다 더 많이 복사하기 때문에 병합 정렬은 제자리에서 작동하지 않는다합니다.
그에 반해 선택 정렬과 삽입 정렬은 어떤 경우라도 배열 요소를 상수 개수 이상 복사하지 않기 떄문에 모두 제자리에서 작동합니다.
저장 공간이 부족하다면, 이 시스템에서는 제자리에서 작동하는 알고리즘이 선호되므로 이런 고려를 해봐야합니다. 이상으로 병합정렬에 대한 개념 이해를 마칩니다.