하노이의 탑 이해 및 재귀를 활용하여 풀기

하노이의 탑

대표적인 재귀 문제인 하노이의 탑, 알아보겠습니다.

 

하노이의 탑 개념

문제 하노이의 탑의 목적은 위 그림과 같습니다.

"한 축에서 다른 한 축으로 고리를 전부 옮겨야합니다"

글로 보고 말로만 들으면 참 쉬워보입니다. 하지만 결코 쉬운 문제는 아닙니다. 아래의 두 규칙이 있기 때문입니다.

1. 한 번에 하나의 원반만 움직일 수 있습니다.
2. 자신보다 작은 원반이 그 아래에 놓일 수 없습니다.

위 규칙때문에 아시아 전설(?)에 따르면 수도승들이 위 문제를 64개의 원반으로 풀어보려고 했다합니다. 만약 이게 풀어진다면 세상이 끝난다고 믿었다고...

 

재귀적으로 풀기

본론으로 들어와 재귀적으로 풀어보겠습니다. 가장 쉬운 경우부터 살펴보겠습니다. 원반이 한 개 있을때, 즉 n=1일 때는 언제는 원반을 다른 축으로 옮길 수 있습니다.

 

원반이 두 개 있을때, 즉 n=2인 경우를 살펴보겠습니다.

 

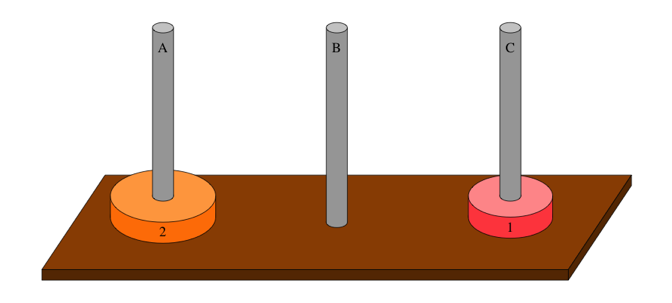
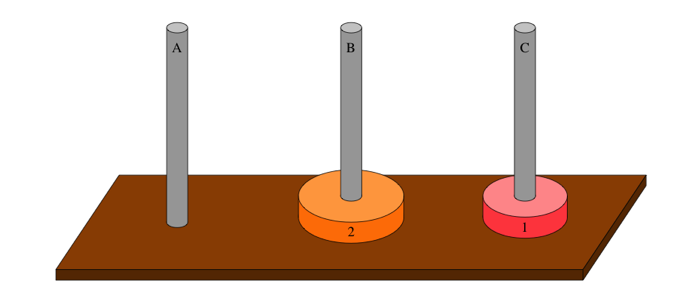
총 3단계만에 축을 옮길 수 있었습니다. 이제 좀 문제가 쉬워보이는 듯 합니다.

 

아래 자바스크립트를 보겠습니다.

var solveHanoi = function(numDisks, fromPeg, toPeg) {
    // base case:  no disks to move
    if(numDisks === 0)
    {
        return 0;   
    }
    // recursive case:
    var sparePeg = hanoi.getSparePeg(fromPeg, toPeg);
    solveHanoi(numDisks-1, fromPeg, sparePeg);
    hanoi.moveDisk(fromPeg, toPeg);
    solveHanoi(numDisks-1, sparePeg, toPeg);
};

우선 탈출 조건을 적습니다. 그 후 나머지 축을 찾는 함수를 실행시켰습니다. 그리고 제일 큰 디스크보다 한 치수 작은 원반을 나머지축으로 옮깁니다. 이 후 원래 축 가장 위에 있는 녀석을 가운데로 옮깁니다. 그리도 다시 한 번 제일 큰 디스크보다 작은 디스크를 나머지 축에서 목표 축으로 옮깁니다.

 

앞서 살펴봤던 2개짜리의 이동방식과 마찬가지 과정을 그립니다. (3단계)

 

이상입니다. 재귀 알고리즘의 과정을 머리로 이해하려고 하면 어려우니, 하위 문제를 구해서 문제를 맞춘다는 느낌으로 풀어야 할 듯 합니다. 일단 하노이의 탑 문제는 여기까지입니다.

 

추 후 백준 알고리즘 中 하노이의 탑 문제로 다시 한 번 풀어보겠습니다.